Accuracy of harmonics amplitude in RTA

[FrenchFan]

Hi John

It took me a while to write these comments.

I would like to know what your policy is regarding the accuracy
of harmonic amplitudes in RTA when you are close to noise (from 15 to 0 dB)
from noise). If this hasn't been corrected, I have version "REW 5.4 Beta 50."

I noticed that in this noise range, the accuracy of harmonic amplitudes
differs slightly depending on whether you are in "coherent averaging" or
"average standard."

In my tool, I have developed my measurement procedure, which
deviates much less from the target values; this procedure is not exceptional.

I'll leave an example here.

If, of course, your interest is low, no response is necessary.

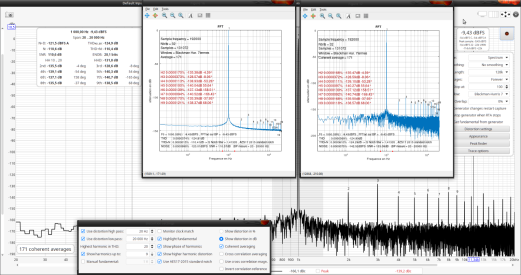
Example ::

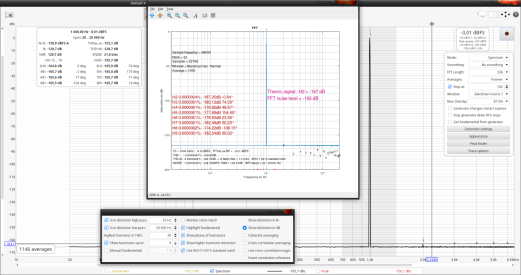
Generated theoretical reference signal:

From -150dB THD to -160dB in 1dB steps.
Noise level in the FFT = -165dB at 32K samples
48KHz sampling rate.

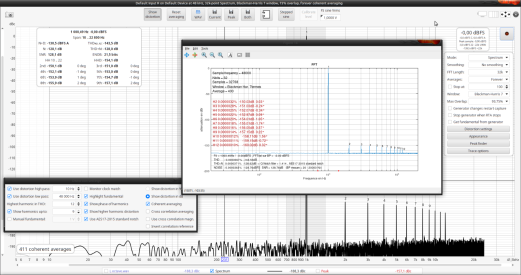
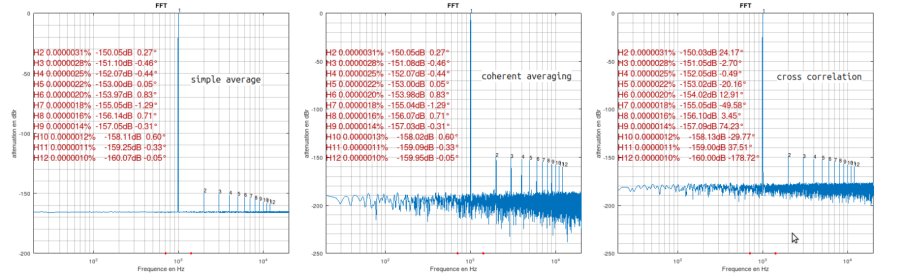
1st REW measurement in "coherent averaging"
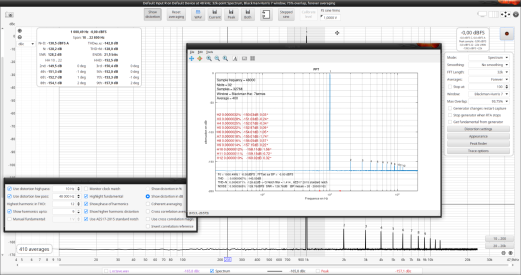
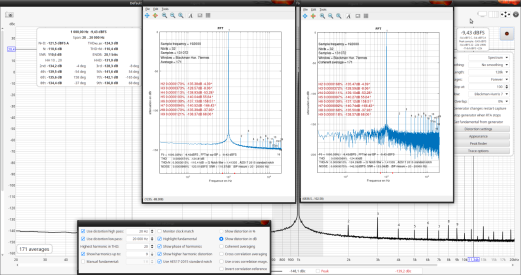
2nd REW measurement in "simple averaging"

To avoid the impact of noise variance, a large number
of averages was chosen.

(Of course, I did hundreds of theoretical examples and direct
measurements before deciding to write this)

In the first case, the THDs align at worst to 0.3dB
In the second case, the THDs align at worst to 1.9dB.

Sincerely

 

[John Mulcahy]

If the system has a common clock for output and input and the tone is on a bin centre, as seems to be the case here, you could use a rectangular window to reduce the contribution of the noise floor for low level harmonics. In other cases the energy within the spreading span of the window should be taken into account, which will include increasingly significant noise contributions when harmonics are less than 10 dB or so above the noise floor.

 

[FrenchFan]

Yes, understood.

With a bin-aligned signal, the square window
greatly improves accuracy.

But regardless of the alignment with bins, you
always have a maximum deviation from the target of 2 dB
for other windows.

My calculation significantly eliminates the
contribution of noise.

Attached is an extreme measurement:

Unaligned frequency = 1000 Hz
H2 = -167 dB
Noise in the FFT = -165 dB

REW Measurement deviation from 167 -> 2.2 dB
DIY Measurement deviation from 167 -> 0.25 dB

A run through "coherent averaging" will show you -167 dB for H2.

Je donne ensuite une comparaison entre toutes les méthodes

 

[John Mulcahy]

That's great, well done. Not sure what you want from me, though.

 

[FrenchFan]

I'll give you my method if you want to integrate it.
I always align with you when it comes to making my tools
as long as I see the same thing.

 

[John Mulcahy]

If you are attempting to identify the noise floor then I'm afraid that becomes very problematic, since noise floors are rarely flat for real systems and can often include non-harmonic distortion contributions. It is similarly not appropriate to exclude harmonics that appear to lie within or below the noise floor since it is possible that they happen to be at the noise floor level.

 

[FrenchFan]

To the first statement, which I agree with anyway, I respond that
I don't identify noise across the entire spectrum but rather within
the bandwidth of the harmonic measurement. I take the minimum noise in
this bandwidth and create a virtual noise of this amplitude in this bandwidth.
I measure its energy, which I subtract from the energy measurement of
the measured harmonic. Therefore, you must always take a tiny bit of noise
around the measurement bandwidth to evaluate the noise below the harmonic.

Regarding the second observation, I showed the measurement of a harmonic of -167dB
with a noise of -165dB, and I still see my harmonic, so I didn't eliminate it,
nor did REW. As a general rule, if the harmonic is <3dB relative to the noise,
you no longer see it.

I'll prepare my method, send it to you, and you can evaluate it if you like
and I mean, if you like.

I'll give you one last example: a measurement on a D10S topping.

 

[dlr]

Comment and question for John. This is a very interesting thread. I'm still on the learning curve on hardware distortion measurement with issues in my rig I haven't resolved due to limitations of my test hardware, in this case the Scarlett 2i2 Gen 4. It's self noise is a problem, but improved by use of the square window on loopback. I've tried using it with the E1DA ADCiso in the loop. This prevents use of the square window and appears to add to the limitations (aside from the ADCiso input impedance issue with the 2i2). The FrenchFan method appears to work with a Blackman-Harris 7 window as well as REW with a square window if I'm reading this right. My question is can this method be included in REW if you could confirm it to work within REW and would it improve the REW results for the case of DAC/ADC not being on the same clock?

 

[John Mulcahy]

I take the minimum noise in
this bandwidth and create a virtual noise of this amplitude in this bandwidth.
I measure its energy, which I subtract from the energy measurement of
the measured harmonic.

I wouldn't use a method that subtracted anything from the observed energy. REW is a little more conservative than it could be, I agree, and so can include more noise than it might. I'll look at that, but analog systems are often much less well behaved with broader distortion peaks and there would be a risk of under-reporting the energy in the harmonic.

Regarding the second observation, I showed the measurement of a harmonic of -167dB
with a noise of -165dB, and I still see my harmonic, so I didn't eliminate it

That comment was based on your image showing reported harmonic levels for H3 etc. that were below the noise floor, I don't think that is appropriate.

Your method is likely well suited to the kinds of systems you are measuring, but REW also gets used for systems where that method would probably not be appropriate.

 

[FrenchFan]

I understand your philosophy,and your comments,
I'm closing the discussion.
But still, thank you for your answers.
Sincerely