Jean Ibarz
New Member
Thread Starter
- Joined
- Jun 23, 2017
- Messages
- 40
More
- Preamp, Processor or Receiver
- Computer
- Main Amp
- Gemini XP3000
- Additional Amp
- Samson SERVO 600
- Other Amp
- Samson SERVO 200 and Yamaha STR-DB840
Hi,
The request is to add a simple arithmetic operator to calculate the maximal frequency amplitude between multiple measurements (two measurements or a set of measurements like the RMS averaging).
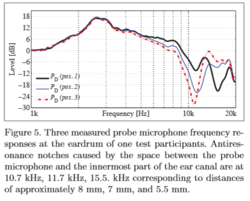
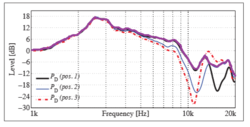
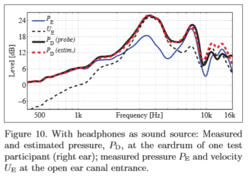
Why ? According to the paper "Estimating head-related transfer functions of human subjects from pressure-velocity measurements" from Marko Hiipakka, Teemu Kinnari and Ville Pulkki, and my understanding of this paper, a way to accurately reproduce the SPL signal at the eardrum is to estimate the total acoustic density in the ear canal. This is because the total acoustic density can be assumed constant in the ear canal and because total acoustic density ~= kinetic energy + potential energy, with kinetic energy being 0 because the eardrum have high impedance and therefore the air particles have no velocity, and the potential energy is directly related to SPL.
As a result, it may be interesting for researchers (or novices like me ) to make multiple measurements with a microphone at different insertion depth in the ear canal. In some measurements, the SPL will be maximal for some frequencies, corresponding to a point in space where the kinetic energy is nearly 0, and hence by estimating the maximal SPL value of each frequencies in the ear canal, one may able to determine the total energy density (up to a squaring of the SPL value and a factor 1/2*rho*c² but this doesn't matter: what matters is the shape of the frequency curve).
) to make multiple measurements with a microphone at different insertion depth in the ear canal. In some measurements, the SPL will be maximal for some frequencies, corresponding to a point in space where the kinetic energy is nearly 0, and hence by estimating the maximal SPL value of each frequencies in the ear canal, one may able to determine the total energy density (up to a squaring of the SPL value and a factor 1/2*rho*c² but this doesn't matter: what matters is the shape of the frequency curve).
I hope you will consider implementing this feature, because I believe that it may be possible that the total energy density would be the physical quantity that should be equalized in a Room, and not the SPL or the spectral average of multiple SPL measurements.
Best regards,
Jean
The request is to add a simple arithmetic operator to calculate the maximal frequency amplitude between multiple measurements (two measurements or a set of measurements like the RMS averaging).
Why ? According to the paper "Estimating head-related transfer functions of human subjects from pressure-velocity measurements" from Marko Hiipakka, Teemu Kinnari and Ville Pulkki, and my understanding of this paper, a way to accurately reproduce the SPL signal at the eardrum is to estimate the total acoustic density in the ear canal. This is because the total acoustic density can be assumed constant in the ear canal and because total acoustic density ~= kinetic energy + potential energy, with kinetic energy being 0 because the eardrum have high impedance and therefore the air particles have no velocity, and the potential energy is directly related to SPL.
As a result, it may be interesting for researchers (or novices like me
I hope you will consider implementing this feature, because I believe that it may be possible that the total energy density would be the physical quantity that should be equalized in a Room, and not the SPL or the spectral average of multiple SPL measurements.
Best regards,
Jean
Last edited: